Abstract

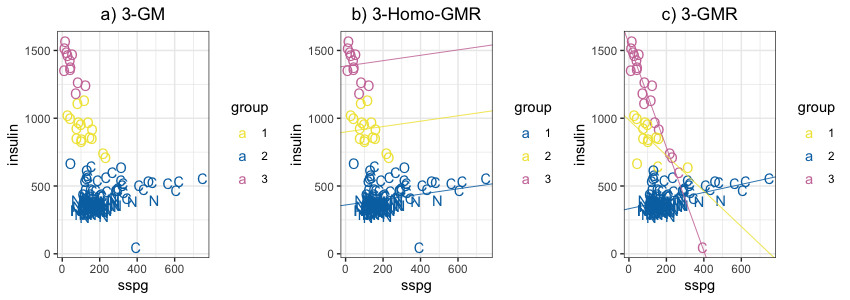
Gaussian mixture model is being increasingly used to cluster the unobserved heterogeneous data. It is common that some covariates are related to the observed outcomes of interests such that they provide valuable information to cluster the response. In order to investigate the covariate effects on the response, we introduced a sequential test within Gaussian mixture regression framework. We first perform an overall hypothesis test on whether the covariate has an effect on the response across all the underlying subpopulations. If null hypothesis of overall test is not rejected, it suggests there is no significant association between two variables. If null hypothesis is rejected, a second hypothesis test will be performed to test on whether the covariate has a homogenous or heterogenous effect on the response across all underlying subpopulations. When carrying out hypothesis tests, the number of underlying mixture components is usually unknown, which generates challenges in the design of testing procedure and the interpretation of testing results. We proposed four methods, Naïve I, II, III and weighted significance procedures that based on likelihood ratio tests to solve this problem, and used criteria such as type I error rate, power and adjusted rand index to investigate the feasibilities of these procedures via simulation studies. Furthermore, the sequential test was applied to the diabetes data, revealing how glucose tolerance impacts insulin concentrations differently with respect to their underlying different groups of subjects that were clustered using Gaussian mixture regression model.